圆锥配合标准的主要内容见GB/T12360—2005。
1 圆锥配合的形式
圆锥配合是通过相互结合的内、外圆锥规定的辅可位置,以形成间隙或过盈的。按确定其轴向位置方法的不同,圆锥配合形成的方式有:
(1)结构型圆锥配合
在结构型圆锥配合中,分为由内、外圆锥的结构确定装配最终位置而获得的配合和由内、外圆锥基准平面间的尺寸确定装配最终位置而获得的配合。上述两种结构方式均可形成间隙配合、过渡配合和过盈配合。图1为由轴肩接触这种结构确定装配最终位置而获得的闻隙配合示例。图2为由结构尺寸a(内、外圆锥基准平面间的尺寸)确定装配最级位置而获得的过盈配合示例。
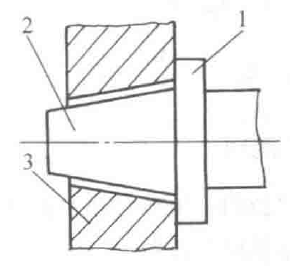
图1 由轴肩接触得到 的间隙配合
1一轴肩 2一外圆锥 3一内圆锥
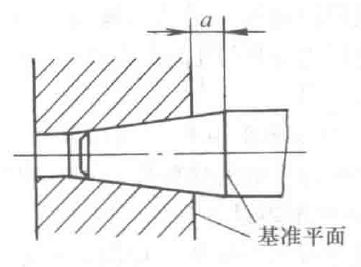
图2 由结构尺寸a得到的过盈配合
(2)位移型圆锥配合
在位移型圆锥配合中,分为由内、外圆锥实际初始位置(Pa)开始、做一定相对轴向位移(Ea)而获得的配合(这种方式既可形成间隙配合,又可形成过盈配合,图3为间隙配合的示例)及由内外圆锥实际初始位置(Pa)开始、施加一定装配力产生轴向位移而获得的配合(这种方式只能形成过盈配合,如图4所示)。
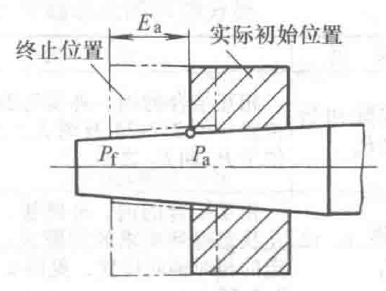
图3 由相对轴向位移Ea得到的间隙配合
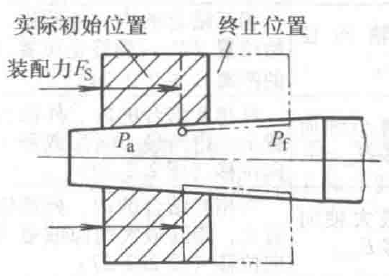
图4 施加一定装配力获得的过盈配合
2 术语和定义
CB/T12360—2005标准规定了以下术语和定义(见表1)。
表1 术语和定义
| 序号 | 术语 | 定义 |
| 1 | 圆锥配合 | 圆锥配合有结构型圆锥配合和位移型圆锥配合两种 |
| 2 | 结构型圆锥配合 | 由圆锥结构确定装配位置,内、外圆锥公差区之间的相互关系,见图1和图2 |
| 3 | 位移型圆锥配合 | 内、外圆锥在装配时做一定相对轴向位移(Ea)确定的相互关系,见图3和图4 |
| 4 | 初始位置P | 在不施加力的情况下,相互结合的内、外圆锥表面接触时的轴向位置 |
| 5 | 极限初始位置P1, P2 | 初始位置允许的界限 P1为内圆锥的下极限圆锥与外圆锥的上极限圆锥的接触位置;P2为内圆锥的上极限圆锥与外圆锥的下极限圆锥的接触位置,见图5 |
| 6 | 初始位置公差Tp | 初始位置允许的变动量,见图5。$T_{P} =\frac{1}{C} \left ( T_{Di} +T_{De} \right ) $ |
| 7 | 实际初始位置Pa | 相互结合的内、外实际圆锥的初始位置(图3及图4),它应于P1和P2之间 |
| 8 | 终止位置Pf | 相互结合的内、外圆锥,为使其终正状态得到要求的间隙或过盈,所规定的相对轴向位置,见图3及图4 |
| 9 | 装配力Fs | 相互结合的内、外圆锥,为在终止位置(Pf)得到要求的过盈所施加的轴向力(图4) |
| 10 | 轴向位移Ea | 相互结合的内、外圆锥,从实际初始位置(Pa)到终止位置(Pf)移动的距离(图3) |
| 11 | 最小轴向位移Eamin | 在相互结合的内、外圆锥的终止位置上,得到最小间隙或最小过盈的轴向位移(图6) |
| 12 | 轴向位移公差Tamax | 在相互结合的内、外圆锥的终正位置上,得到最天间隙或最大过益的辅向位移(图6) |
| 13 | 轴向位移公差TE | 轴向位移允许的变动量,见图6 TE = Eamax – Eamin |
| 14 | 圆锥直径配合量TDf | 圆锥配合在配合直径上允许的间隙或过盈的变动量 |
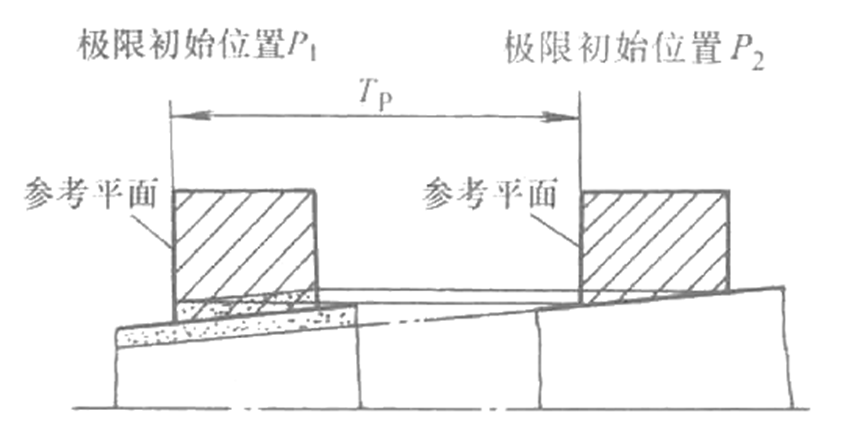
图5 极限初始位置和初始位置公差
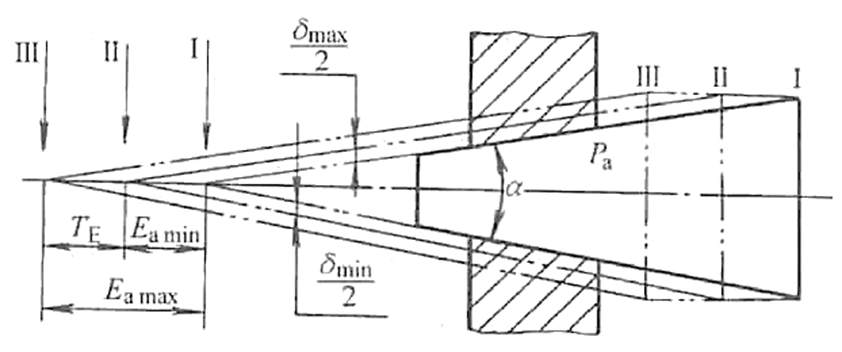
图6 轴向位移及其公差
I一实际初始位置 Ⅱ一最小过盈位置 Ⅲ一最大过盈位置
3 圆锥配合的一般规定
1)结构型圆锥配合推荐优先采用基孔制。