常用数学公式

1 代数

1.1 二项式公式、多项式公式和因式分解

1.1.1 二项式公式

1.1.2 多项式公式

1.1.3 因式分解

1.2 指数和根式

1.2.1 指数

1.2.2 根式

1.3 对数

1.3.1 运算法则

1.3.2 常用对数和自然对数

1.4 不等式

1.4.1 代数不等式

1.4.2 三角不等式

1.4.3 含有指数、对数的不等式

1.5 代数方程

1.5.1 一元方程的解

1.5.2 一次方程组的解

1.6 级数

1.6.1 等差级数

1.6.2 等比级数

1.6.3 一些级数的前n项和

1.6.4 一些特殊级数的和

1.6.5 二项级数

1.6.6 指数函数和对数函数的幂级数展开式

1.6.7 三角函数和反三角函数的幂级数展开式

1.6.8 双曲函数和反双曲函数的幂级数展开式

1.7 复数和傅里叶级数

1.7.1 复数

1.7.2 傅里叶级数

1.8 行列式和矩阵

1.8.1 行列式

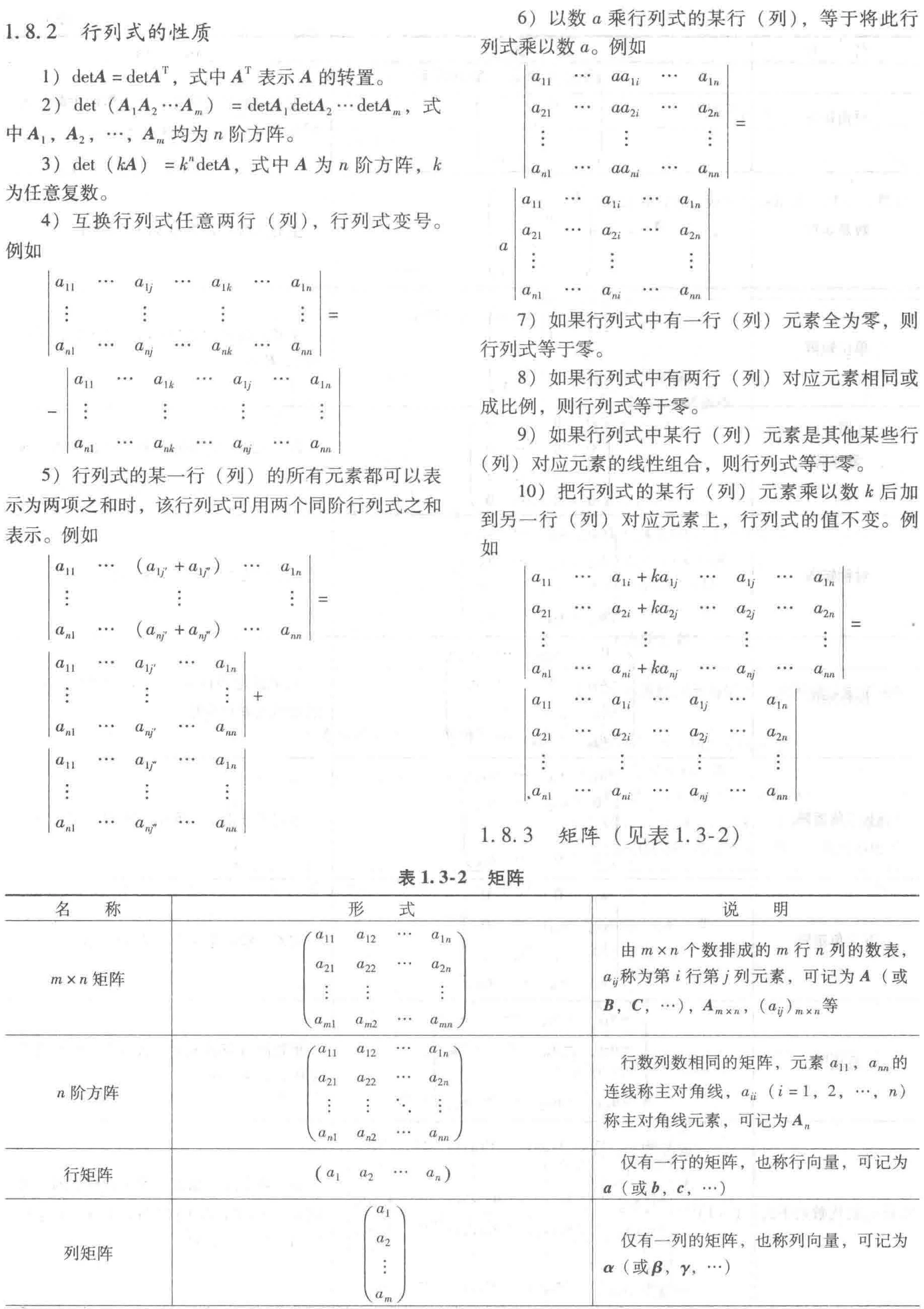
1.8.2 行列式的性质

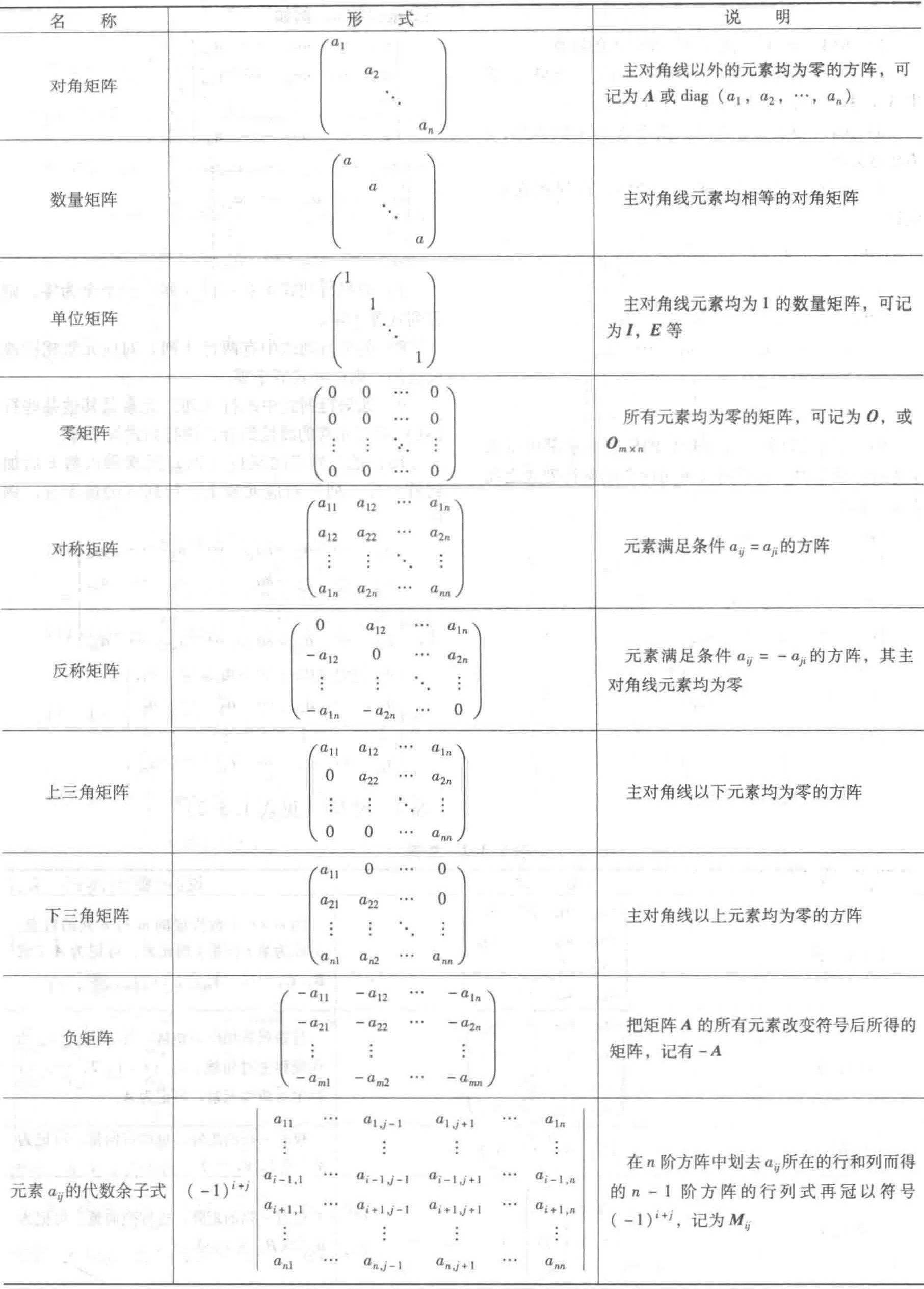
1.8.3 矩阵

1.8.4 矩阵的运算

1.8.5 初等变换、初等方阵及其关系

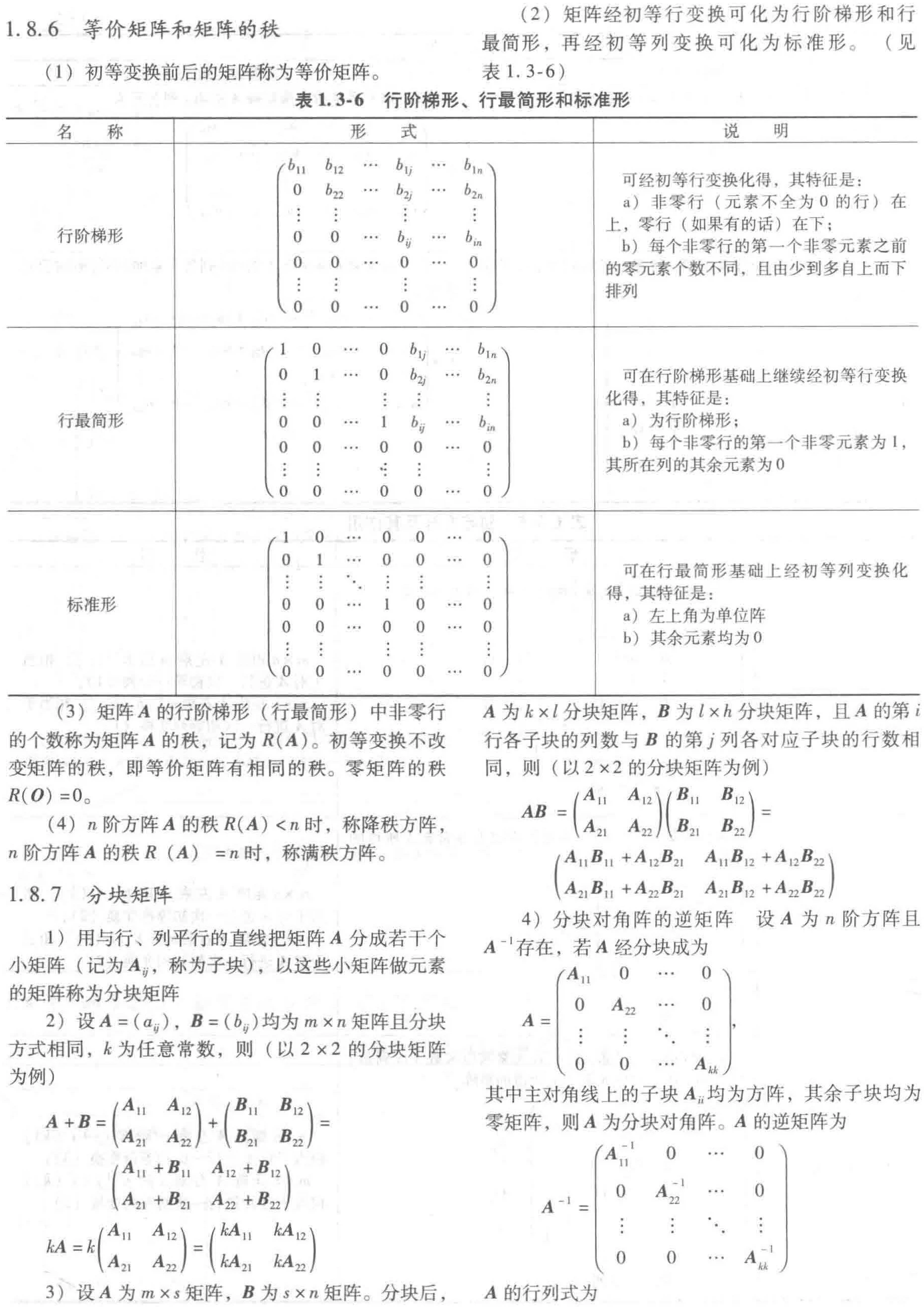
1.8.6 等价矩阵和矩阵的秩

1.8.7 分块矩阵

1.9 线性方程组

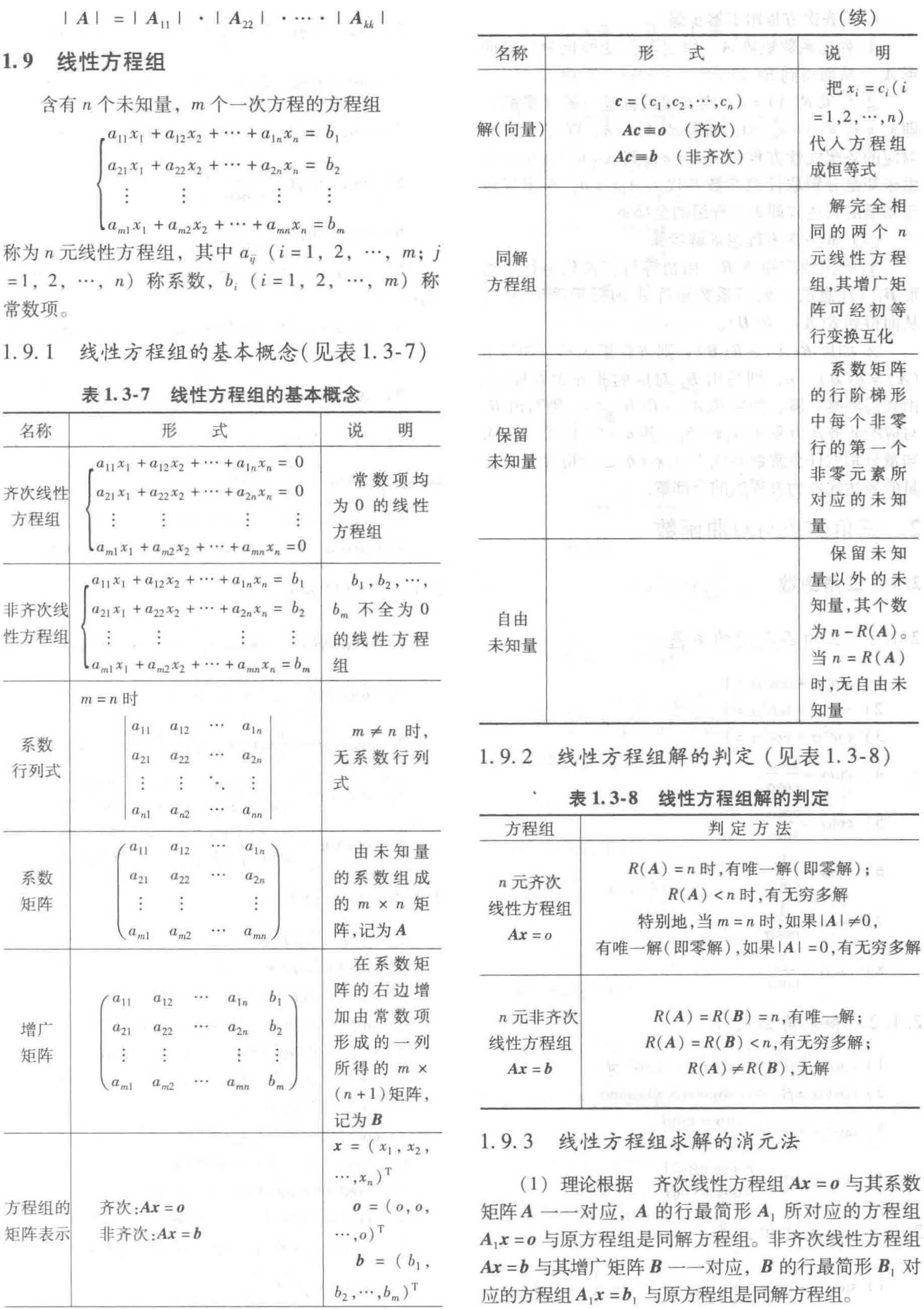
1.9.1 线性方程组的基本概念

1.9.2 线性方程组解的判定

1.9.3 线性方程组求解的消元法

2 三角函数与双曲函数

2.1 三角函数

2.1.1 三角函数间的关系

2.1.2 和差角公式

2.1.3 和差化积公式

2.1.4 积化和差公式

2.1.5 倍角公式

2.1.6 半角公式

2.1.7 正弦和余弦的幂

2.1.8 三角形

2.2 反三角函数间的关系

2.3 双曲函数

2.3.1 双曲函数间的关系

2.3.2 反双曲函数的对数表达式

2.3.3 双曲函数和三角函数的关系

3 平面曲线与空间图形

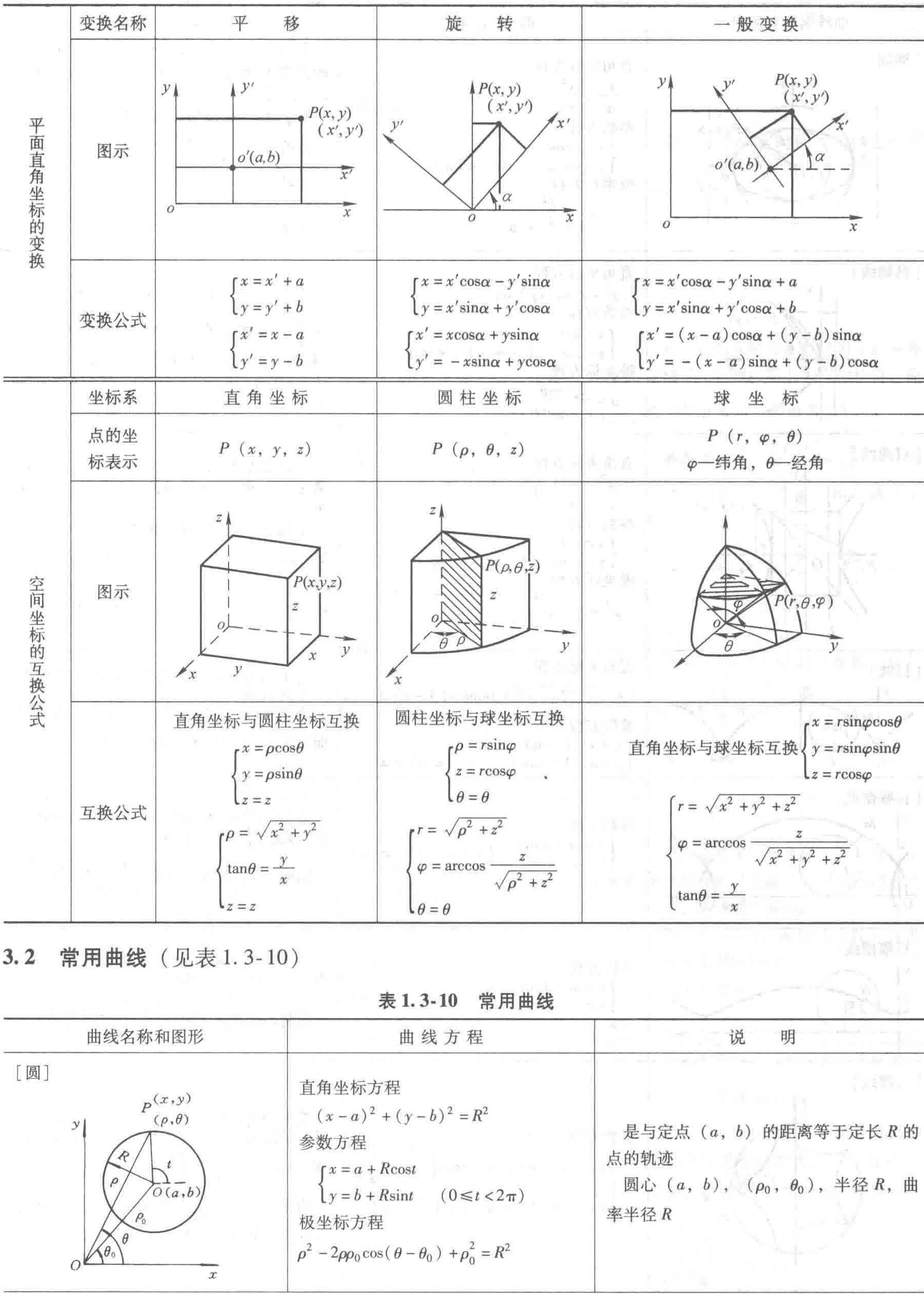
3.1 坐标系及坐标变换

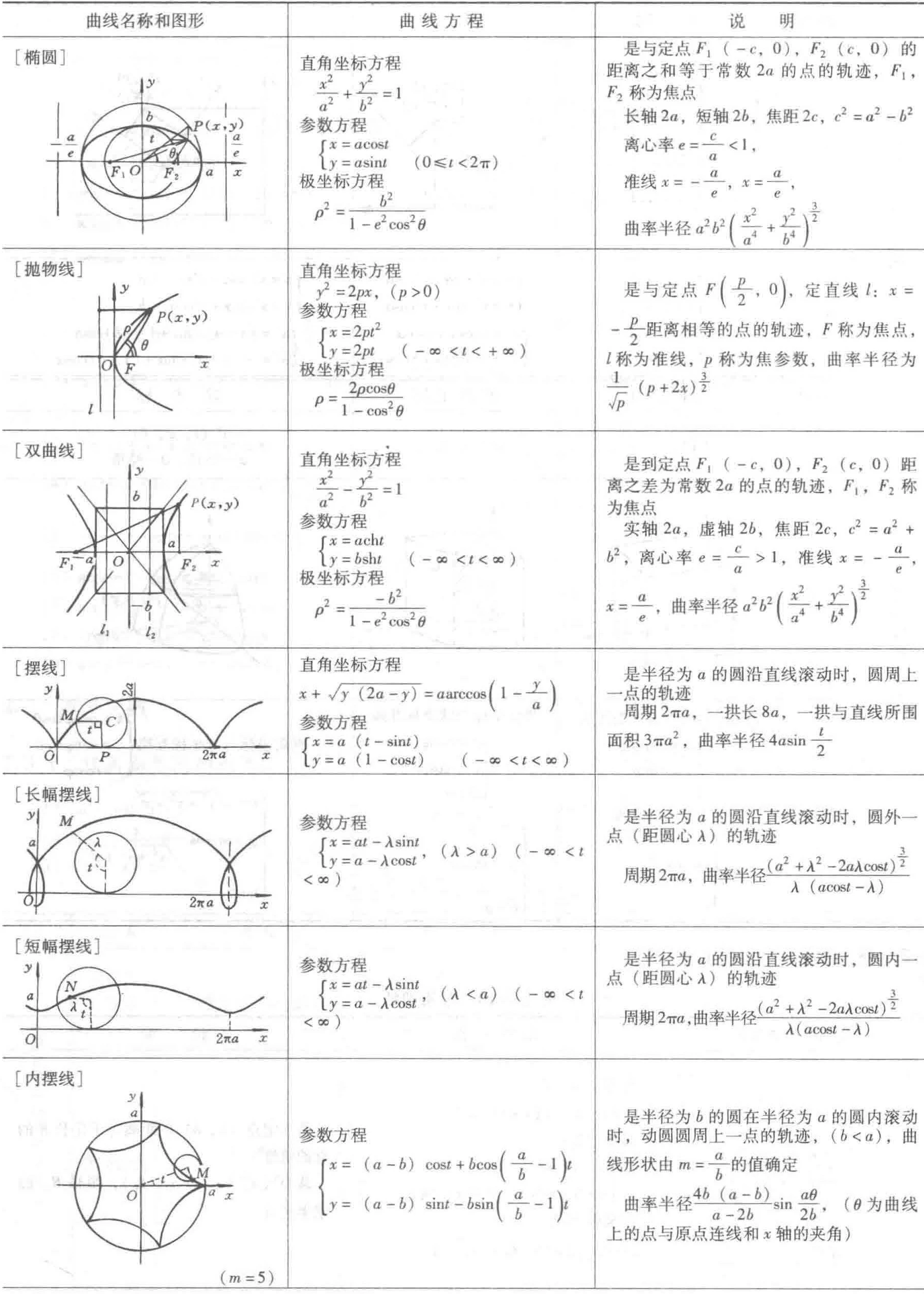
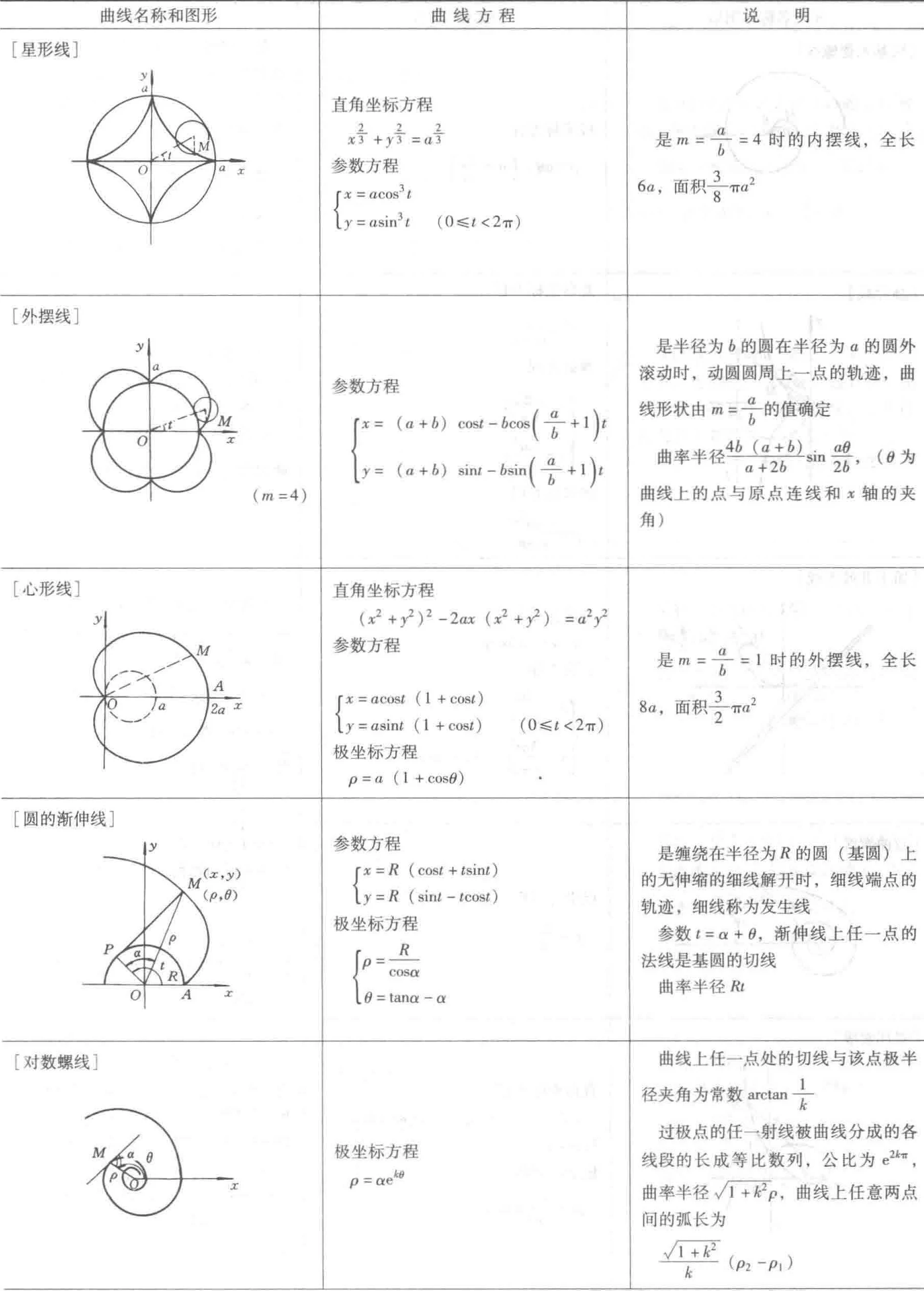
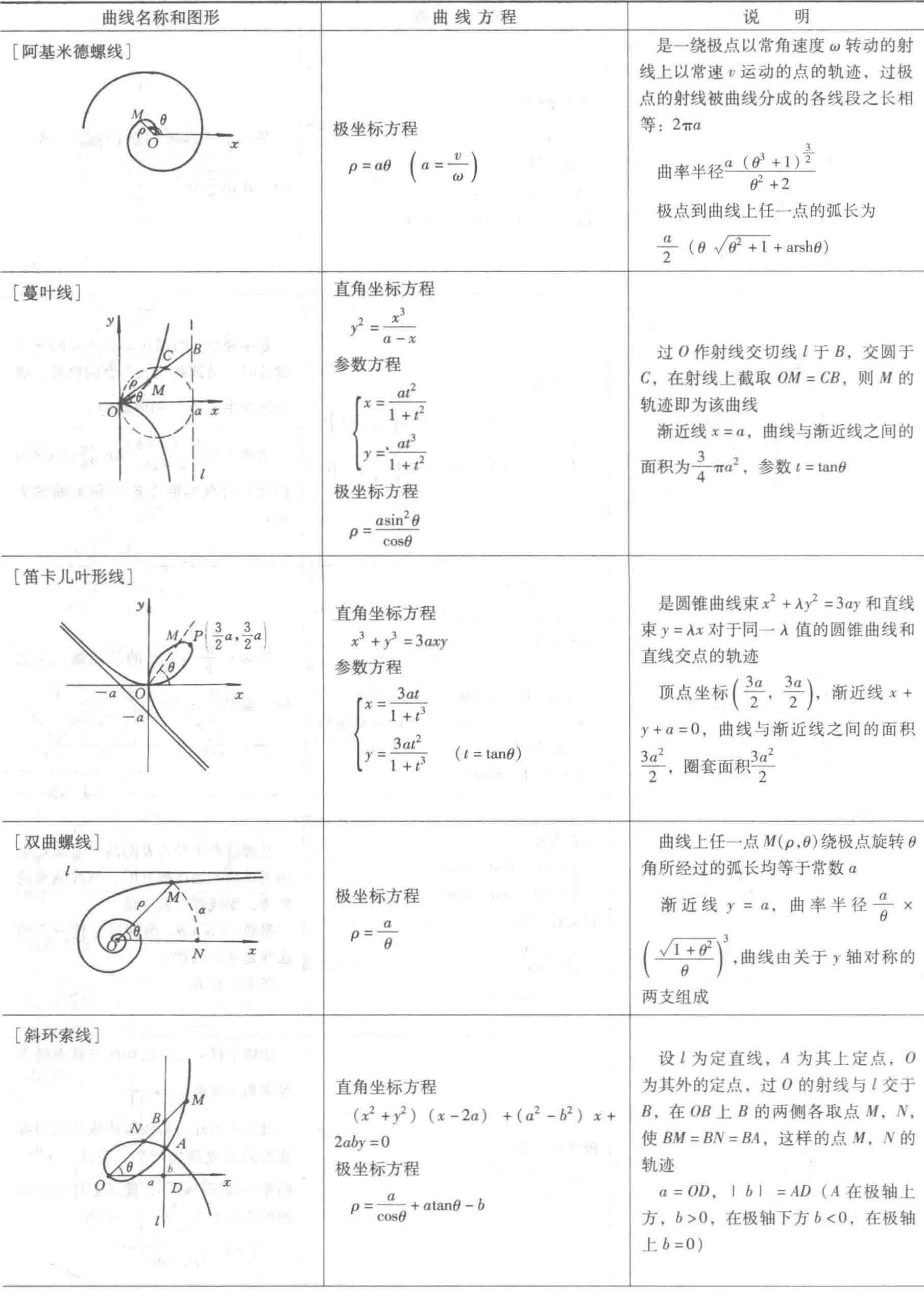
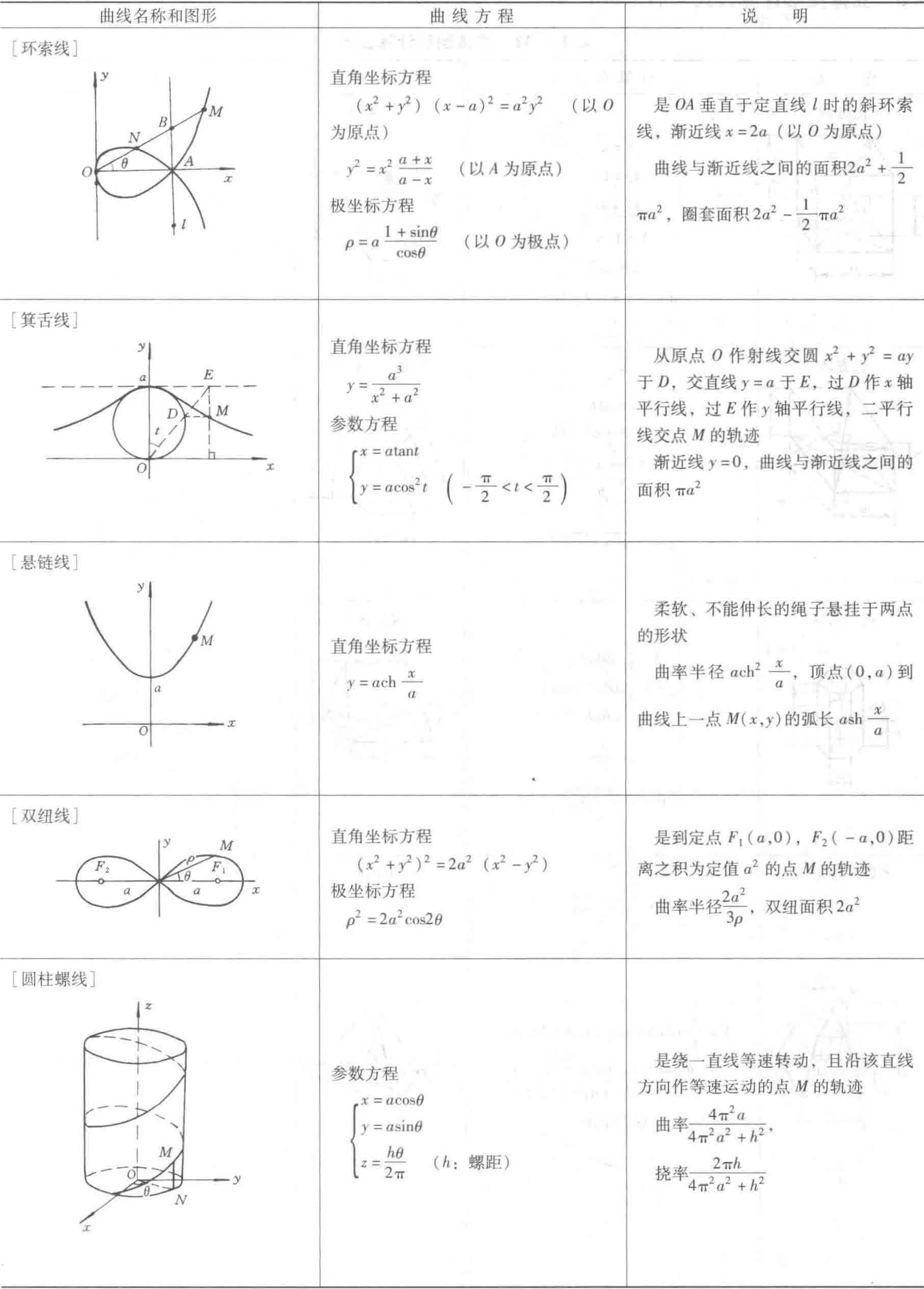
3.2 常用曲线

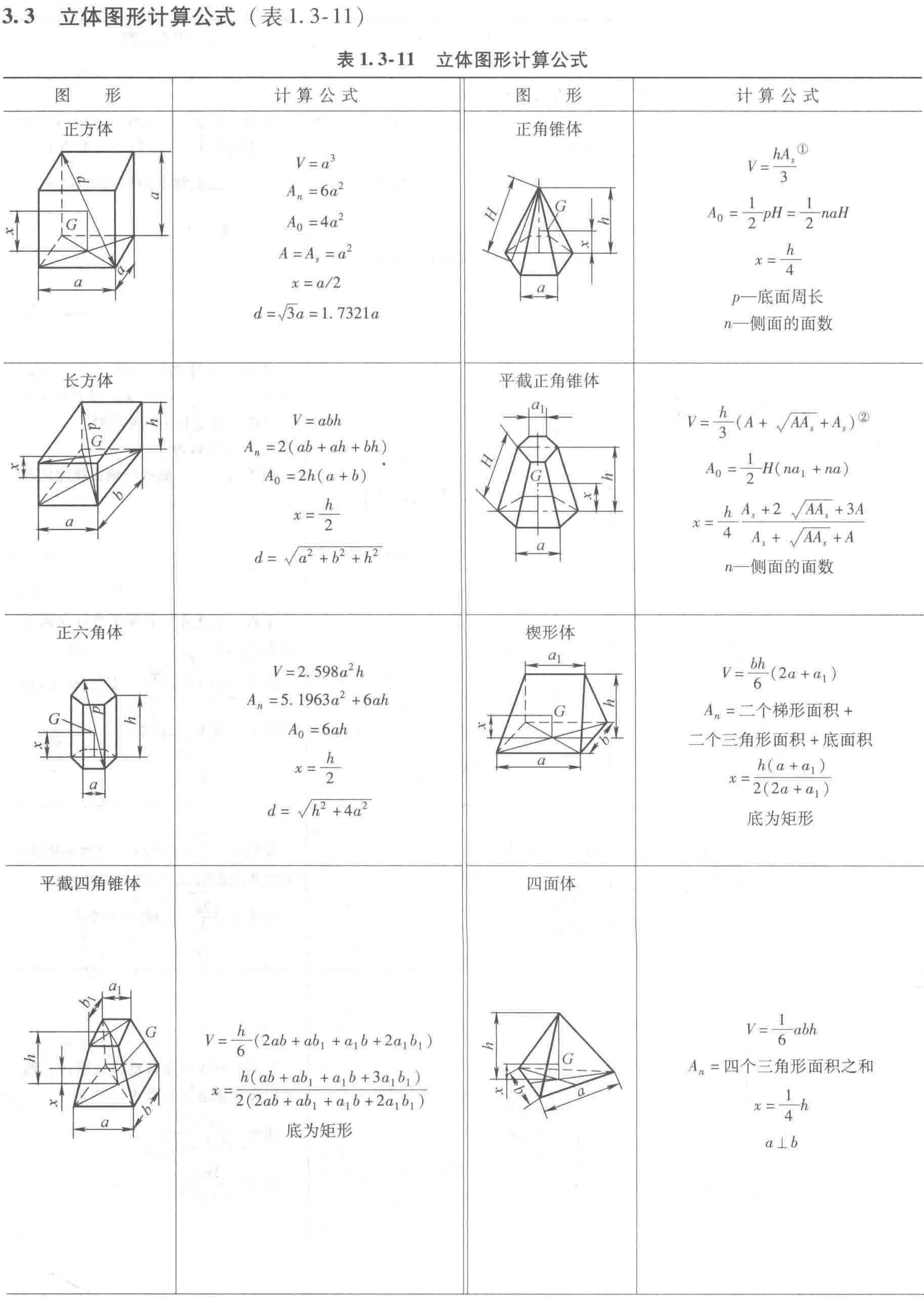
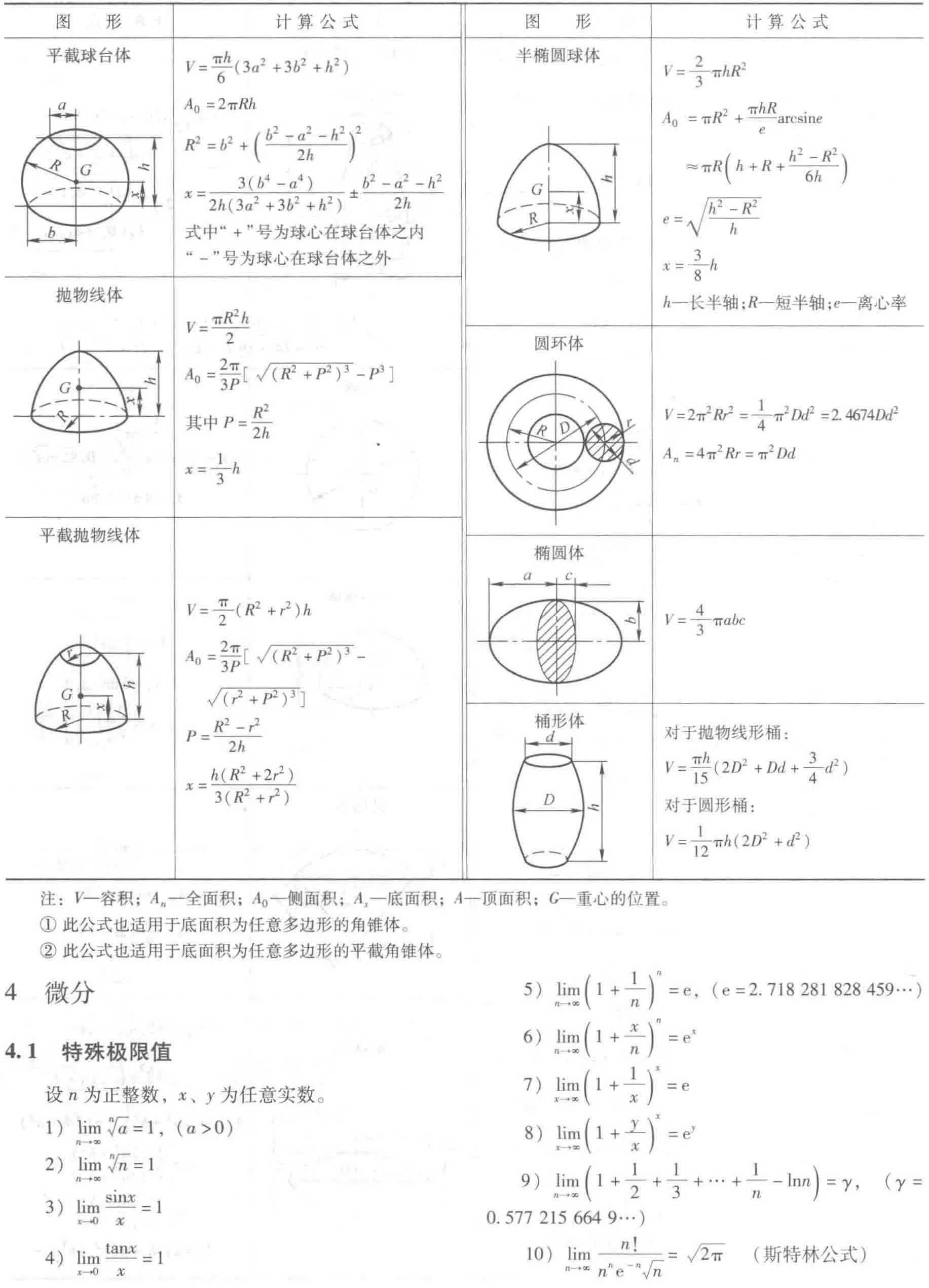
3.3 立体图形计算公式

4 微分

4.1 特殊极限值

4.2 导数

4.2.1 导数符号

4.2.2 求导法则

4.2.3 基本导数公式

4.2.4 简单函数的高阶导数公式

4.3 泰勒公式和马克劳林公式

4.4 曲线形状的导数特征

4.5 曲率和曲率中心

4.6 曲线的切线和法线

5 积分

5.1 不定积分

5.1.1 不定积分法则

5.1.2 常用换元积分法

5.1.3 基本积分公式

5.1.4 有理函数的积分

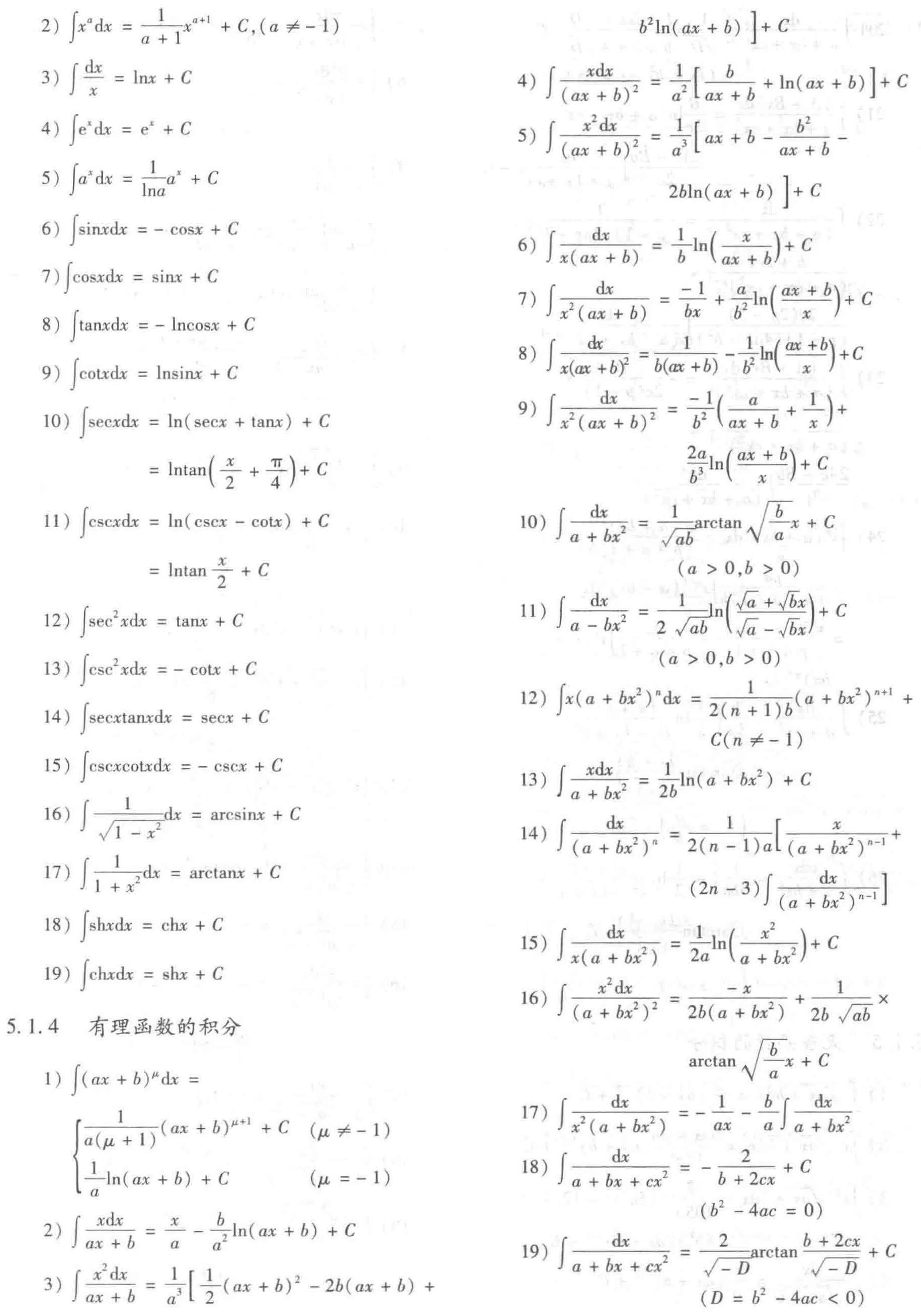
5.1.5 无理函数的积分

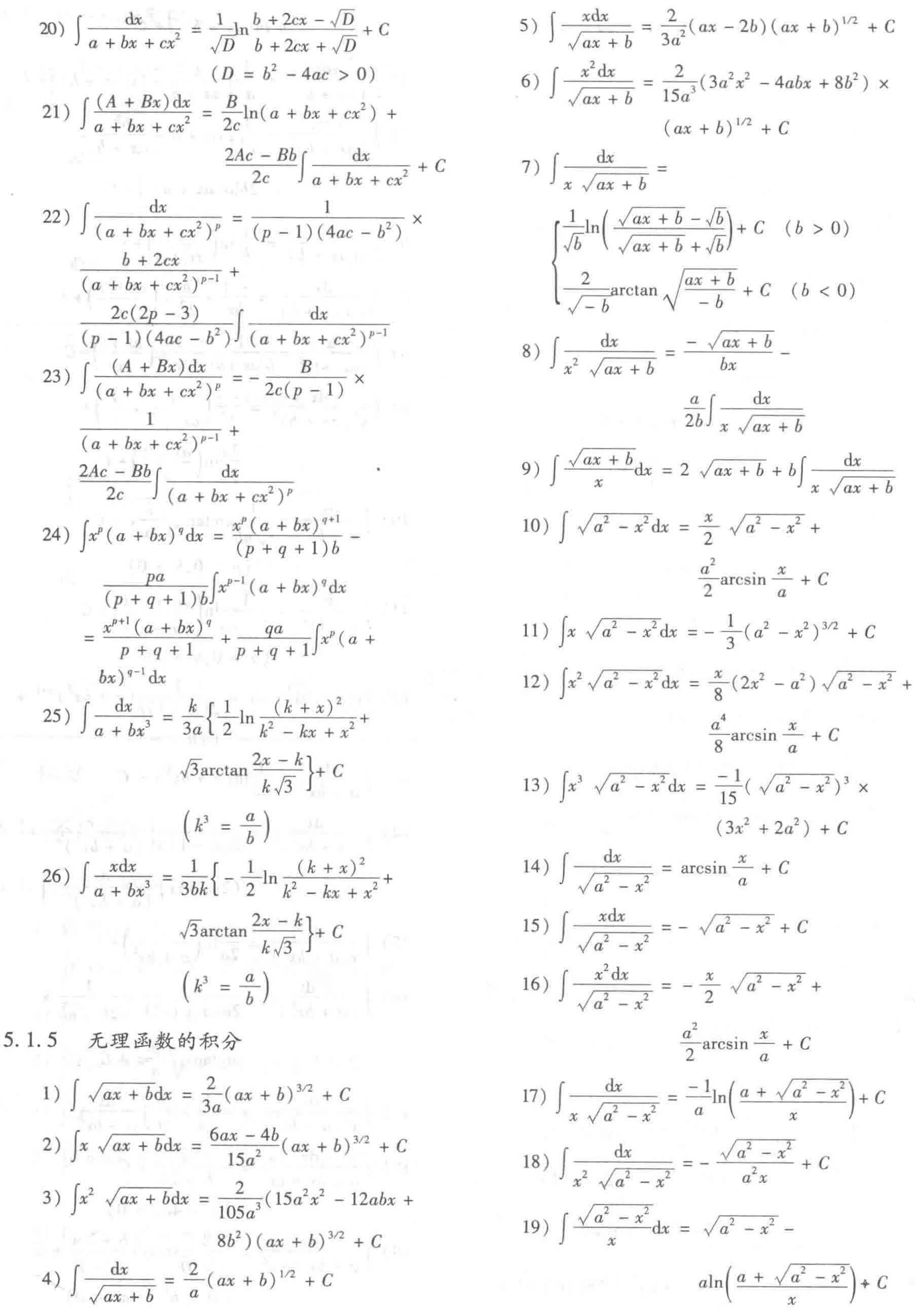
5.1.6 超越函数的积分

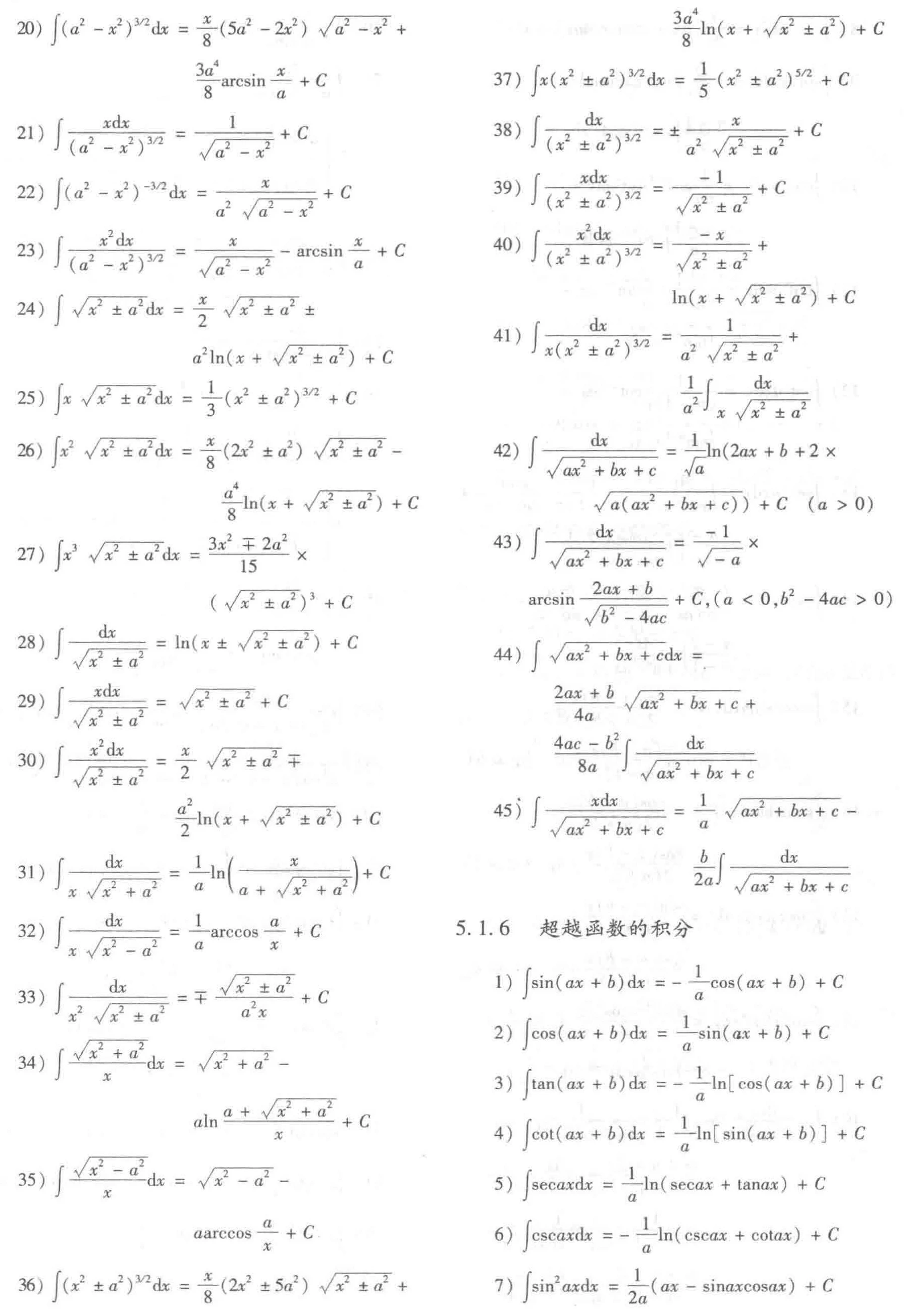
5.2 定积分和反常积分

5.2.1 定积分一般公式

5.2.2 反常积分

5.2.3 重要定积分和反常积分公式

6 常微分方程

6.1 一阶常微分方程

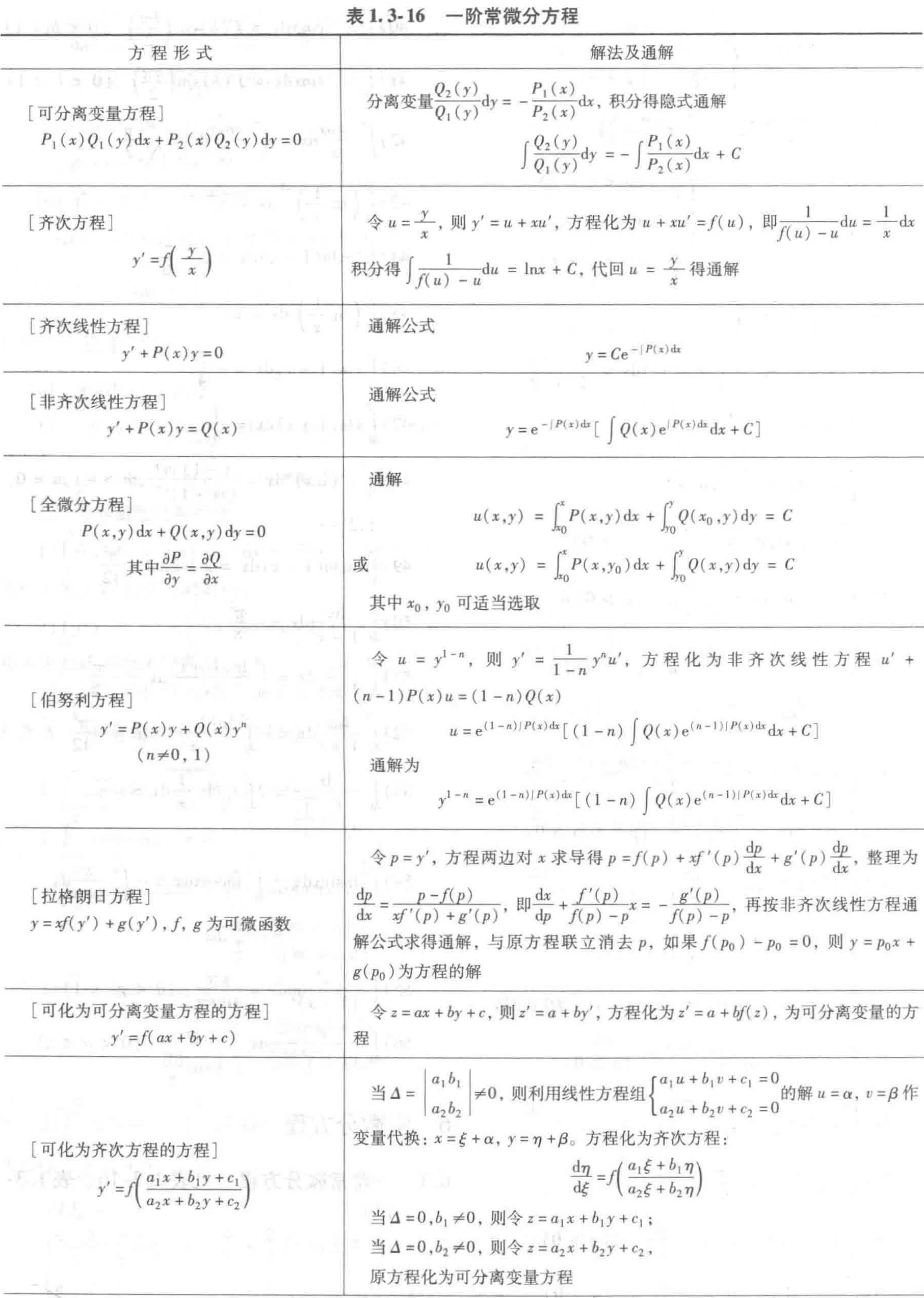
6.2 二阶常微分方程

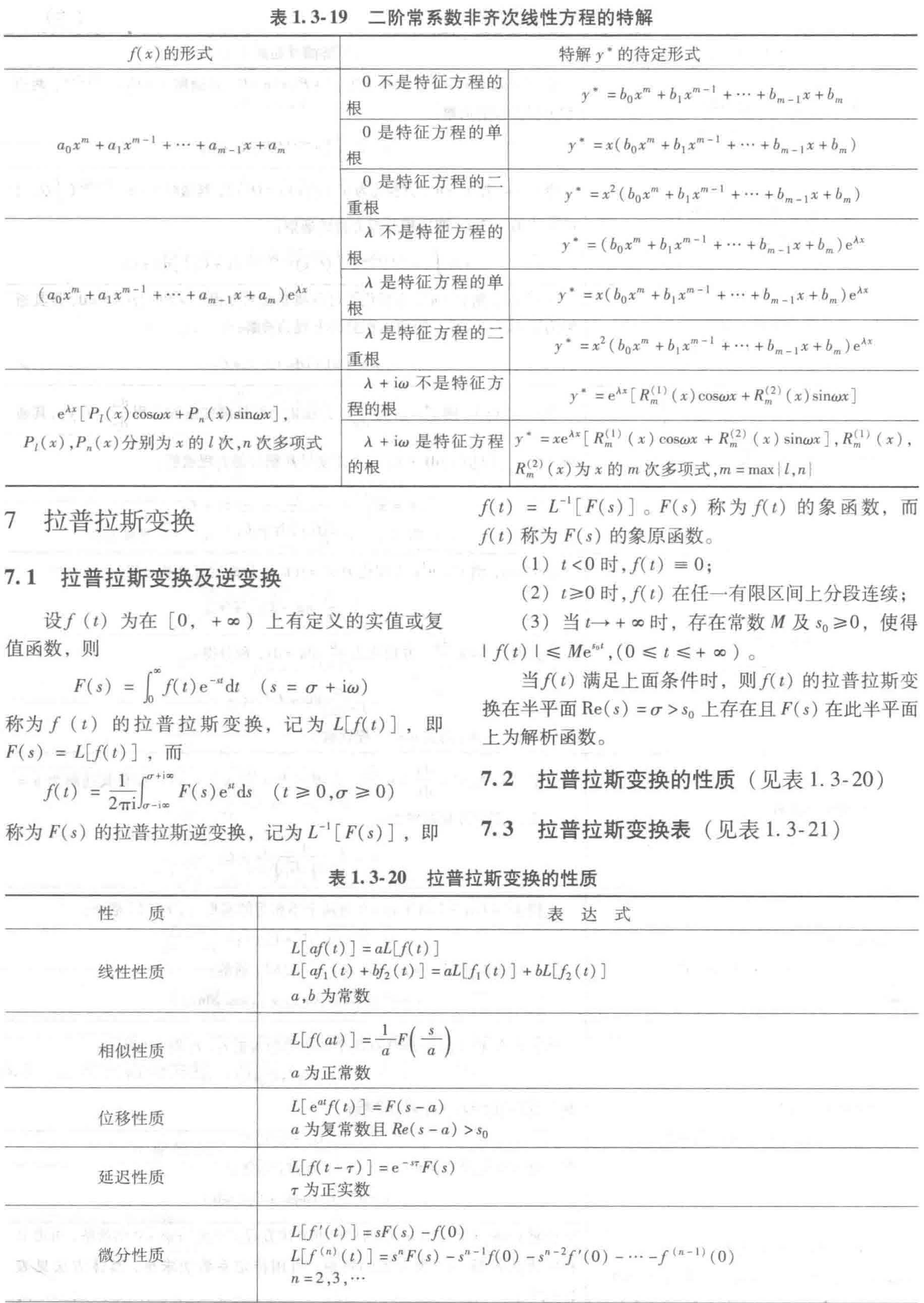
7 拉普拉斯变换

7.1 拉普拉斯变换及逆变换

7.2 拉普拉斯变换的性质

7.3 拉普拉斯变换表

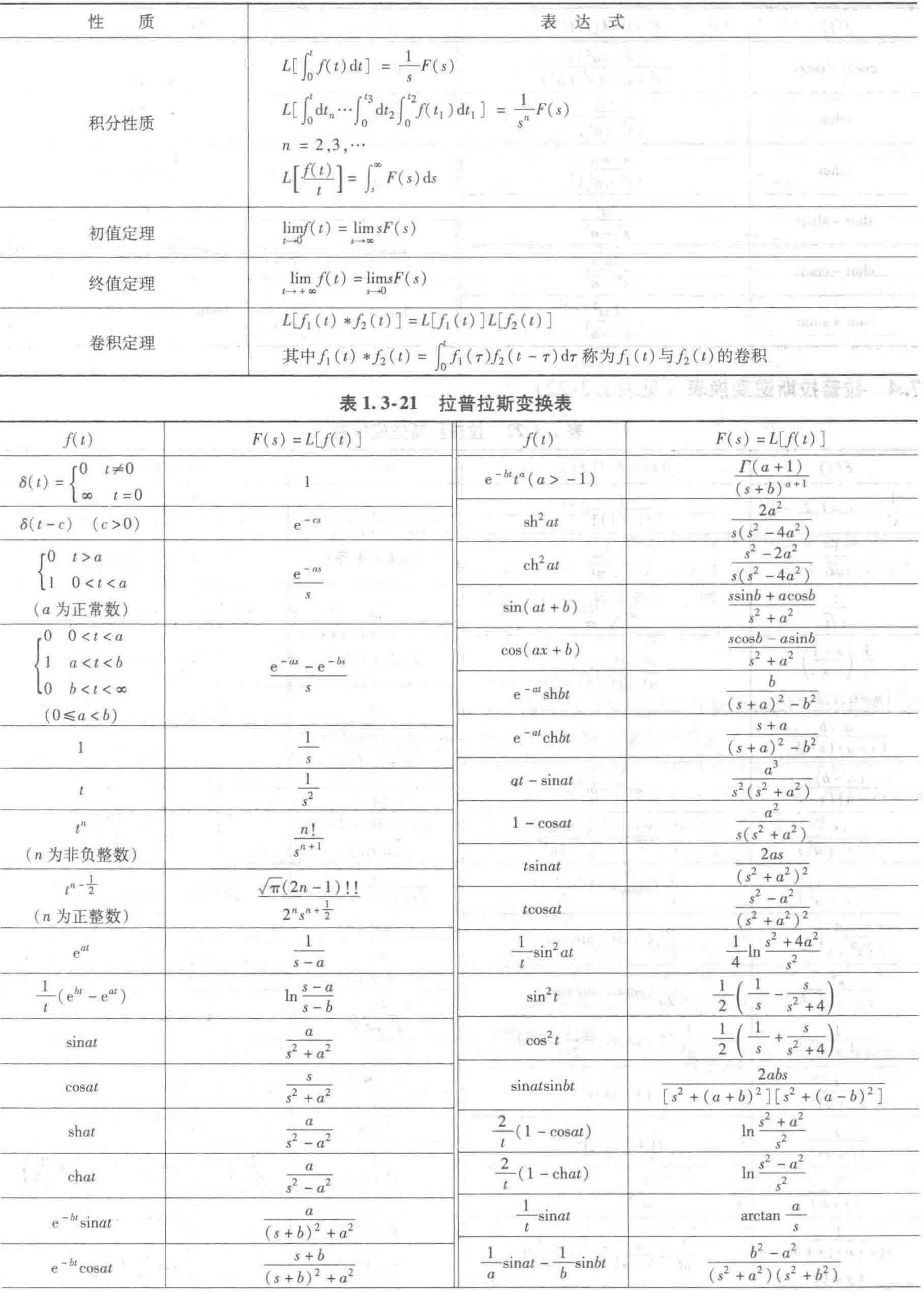
7.4 拉普拉斯逆变换表

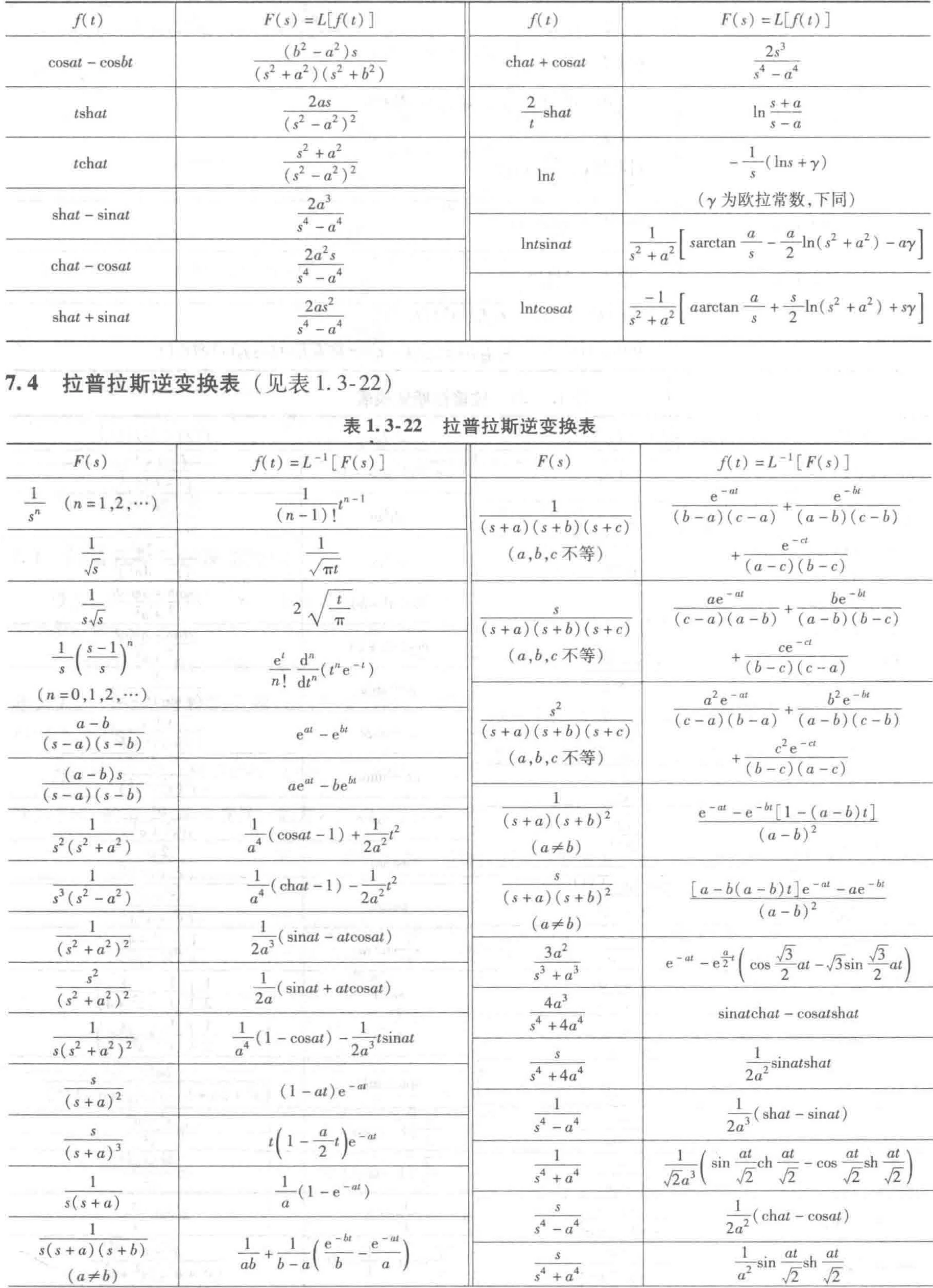
7.5 拉普拉斯变换的应用

7.5.1 常系数线性微分方程的定解问题

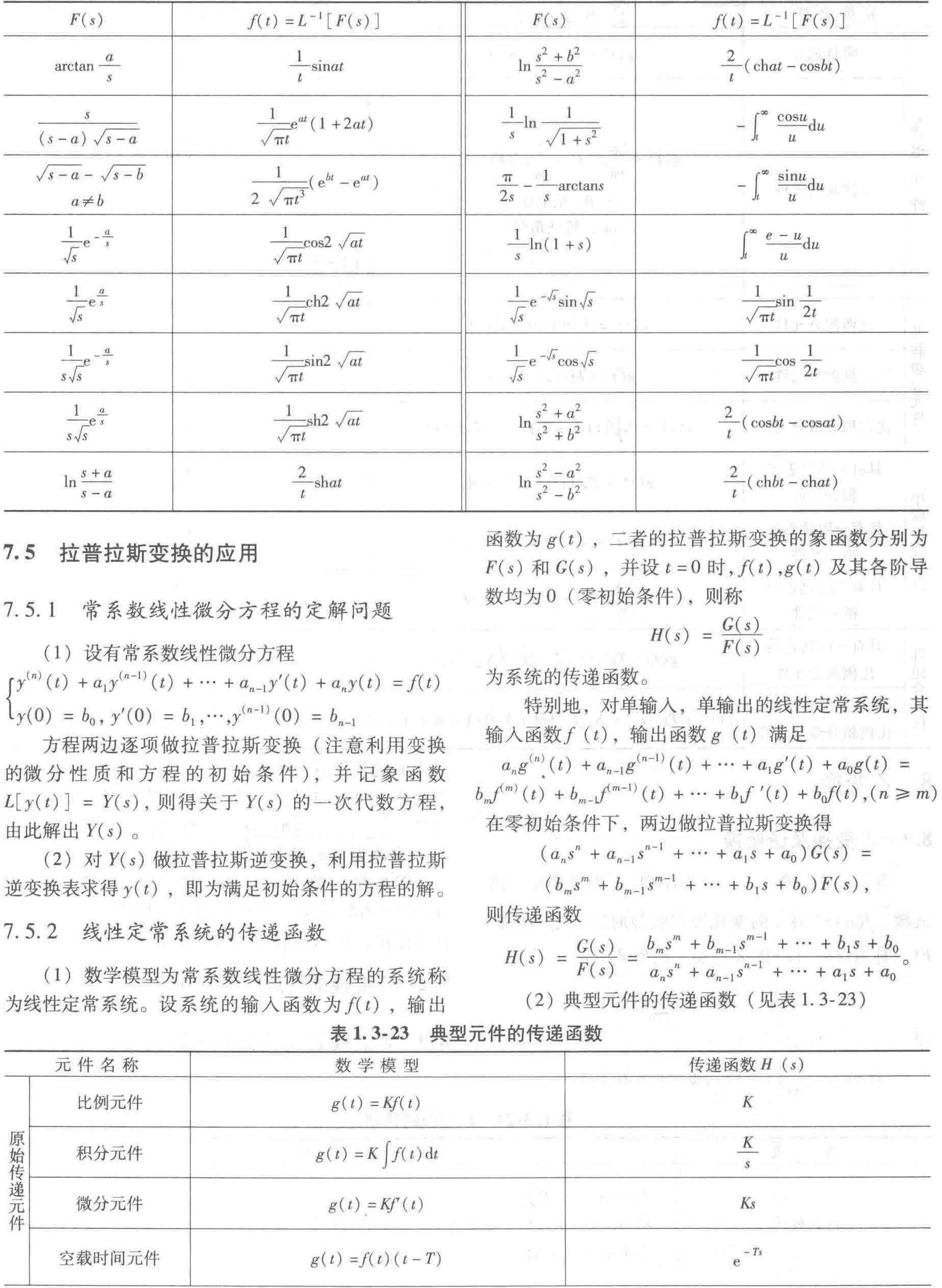
7.5.2 线性定常系统的传递函数

8 Z变换

8.1 Z变换及逆变换

8.2 Z变换的性质

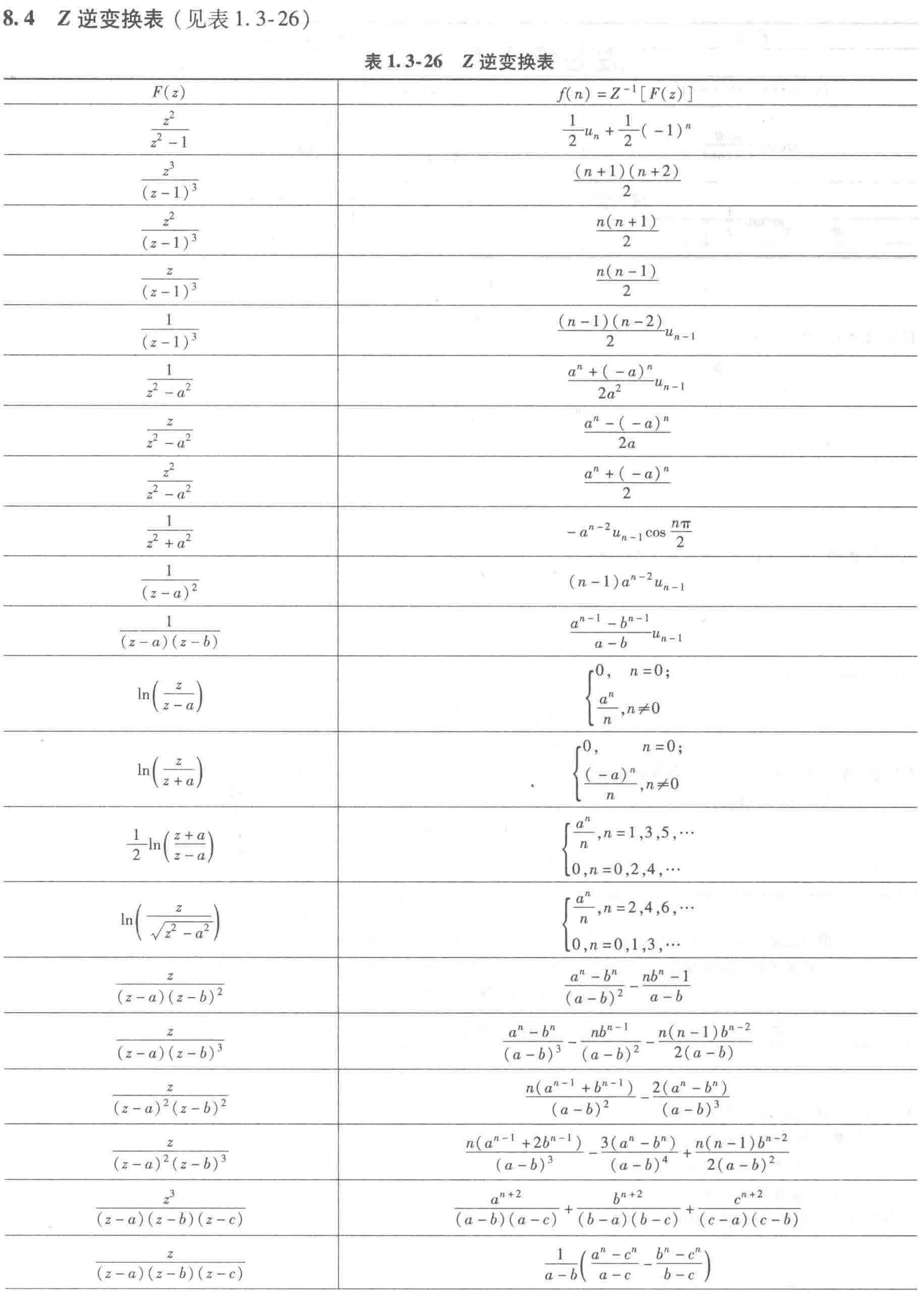
8.3 Z变换表

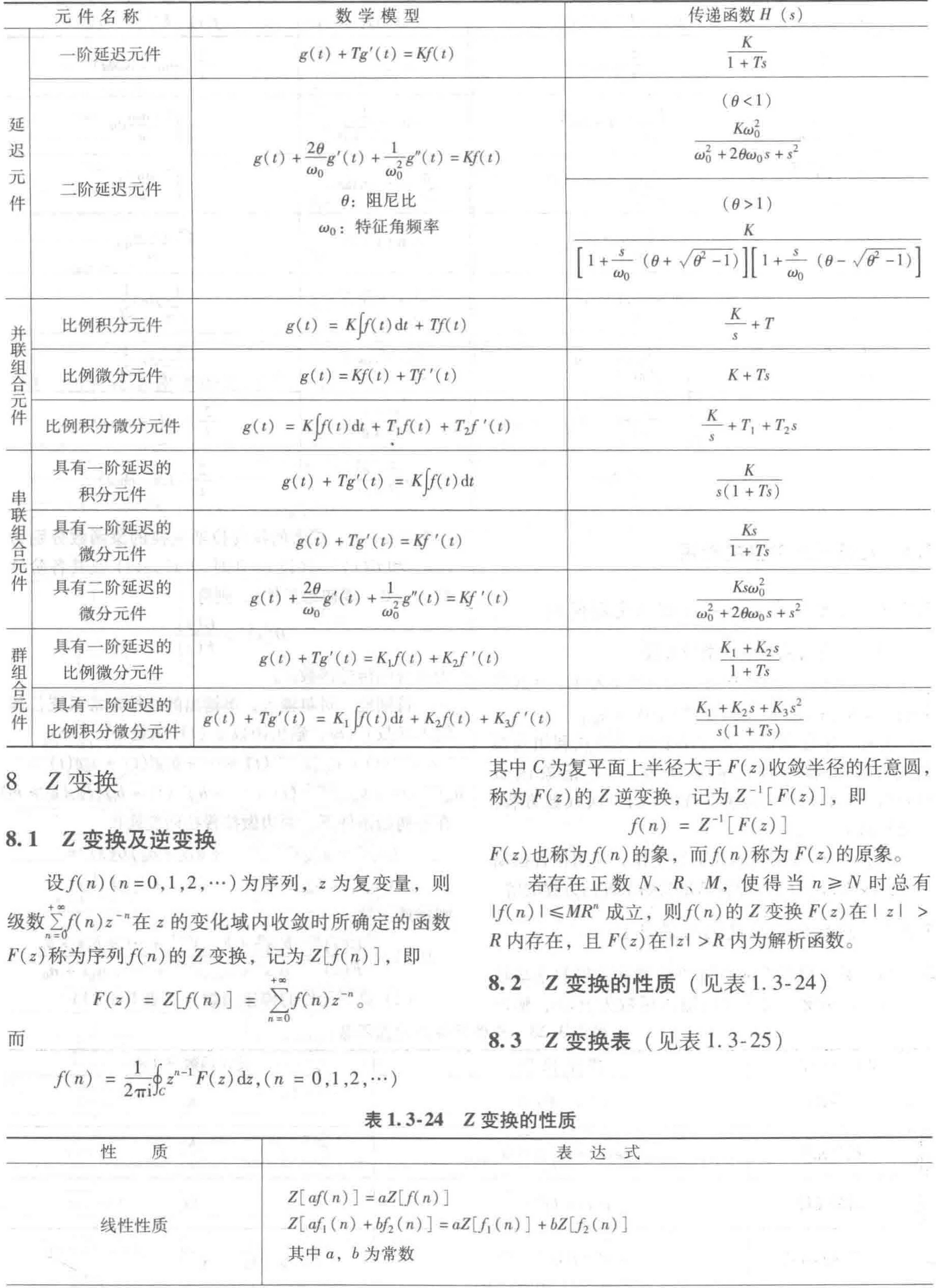
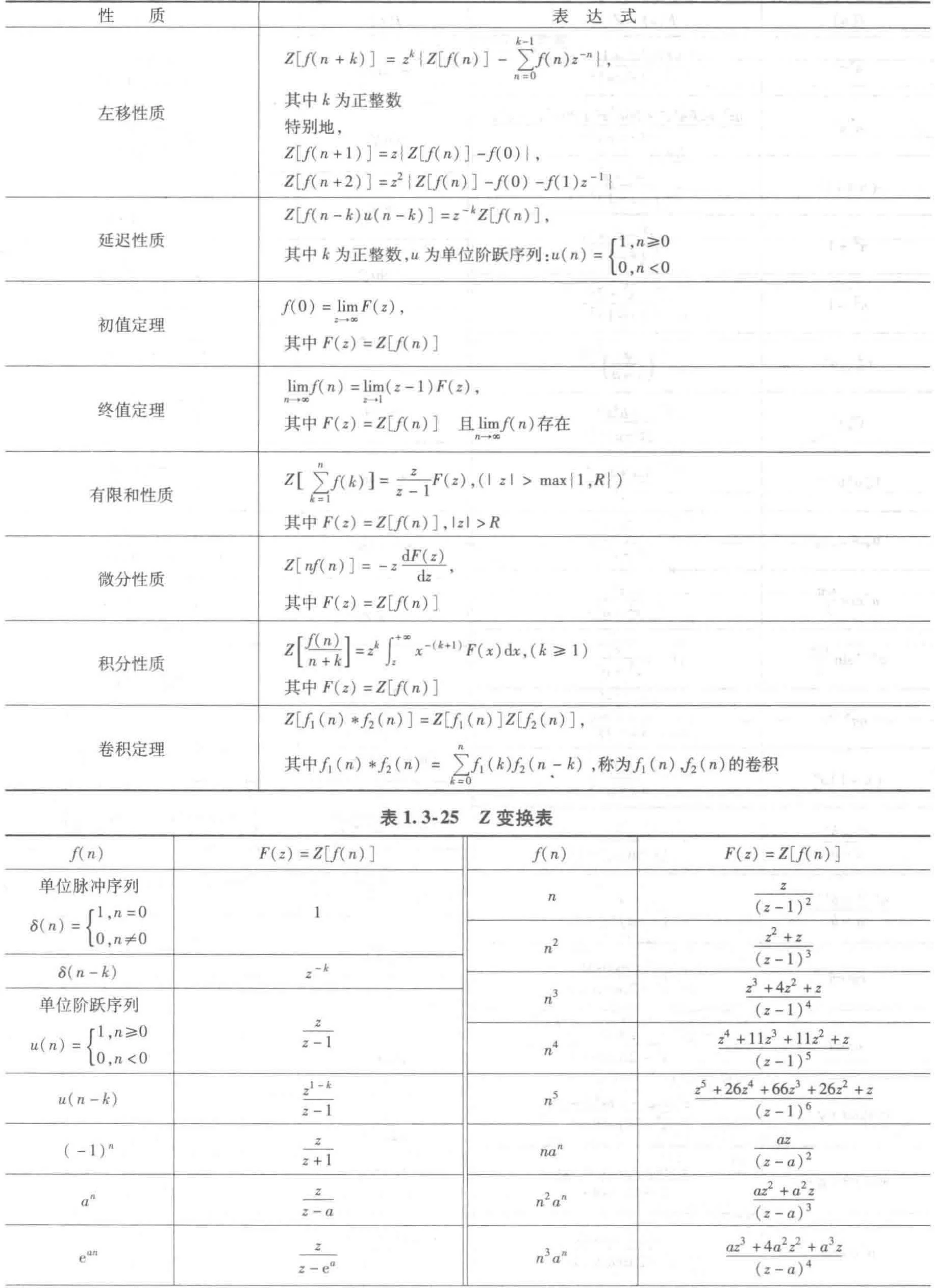
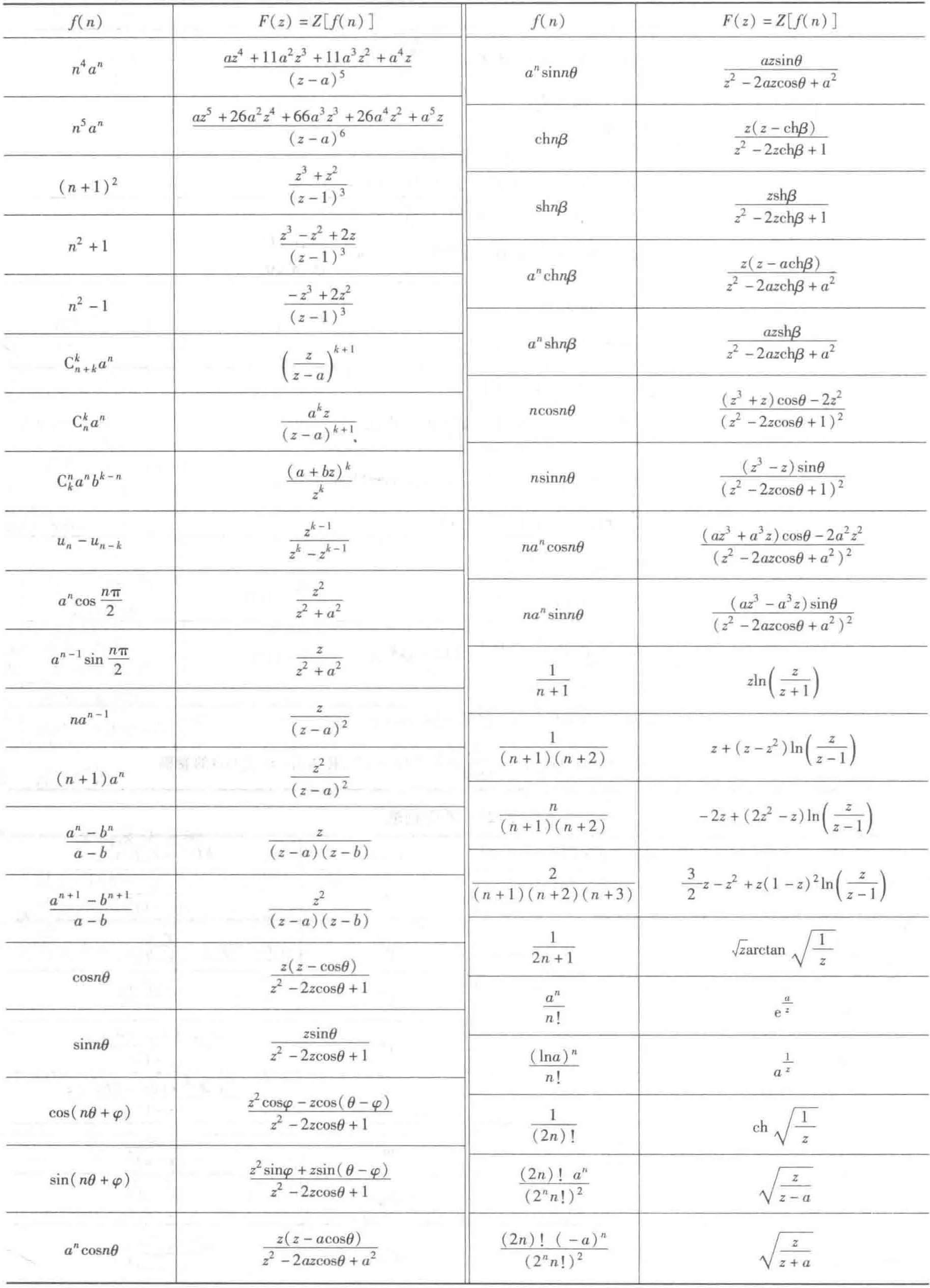
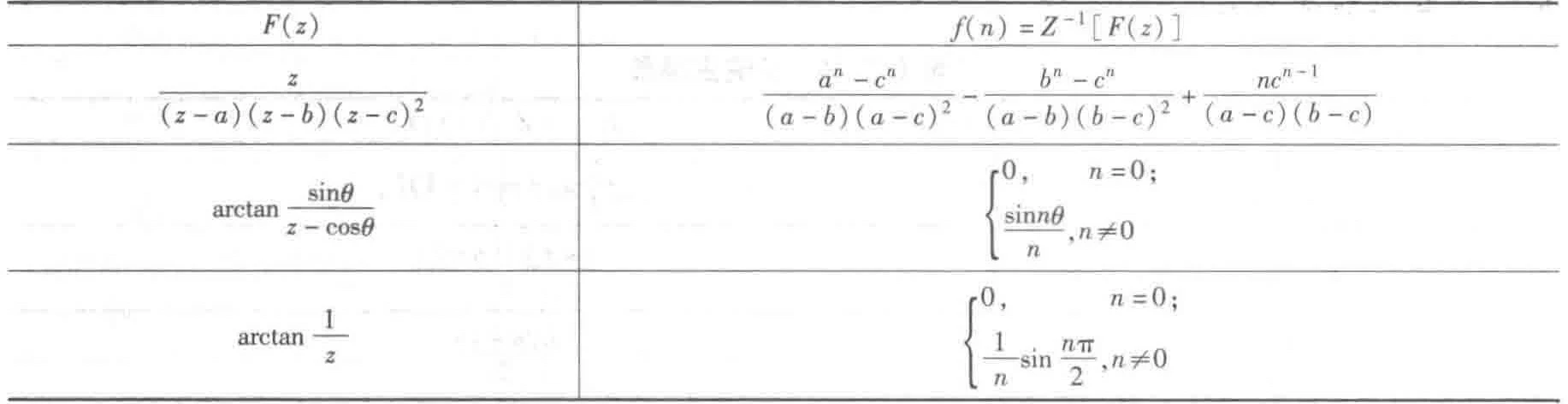
8.4 Z逆变换表